Don't forget your statement of sources. Remember to list any outside reading you consulted for problem 3d.
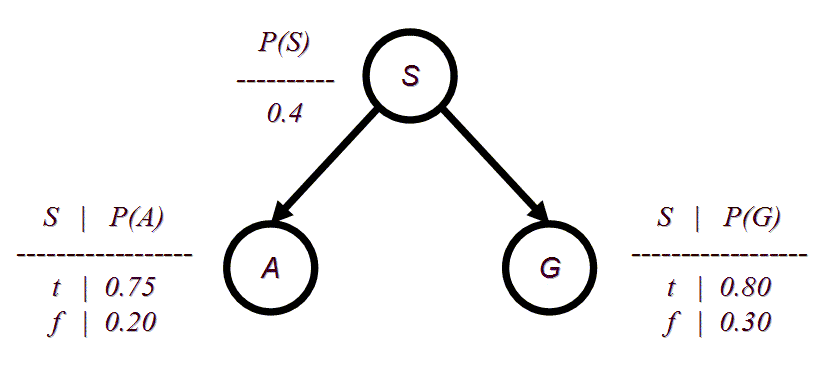
A CMSC 471 student notices that people who drive SUVs (S) consume
large amounts of gas (G) and are involved in more accidents (A) than the national
average. In this problem, uppercase letters
denote the variable names, lowercase values denote the variables with value.
For example, P(a, ~s) is the same thing as
P(A = t, S = f). She has constructed the following
Bayesian network:

(a) (5 pts) Compute P(a, ~s, g) using the chain rule.
(b) (10 pts.) Compute P(a) using inference by enumeration.
(c) (10 pts.) Using conditional independence, compute P(~g, a | s) and P(~g, a | ~s). Then use Bayes' rule to compute P(s | ~g, a).The enterprising student notices that two types of
people drive SUVs: people from California (C) and people with large families
(F). After collecting some statistics, the student arrives at the following
form for the BN:
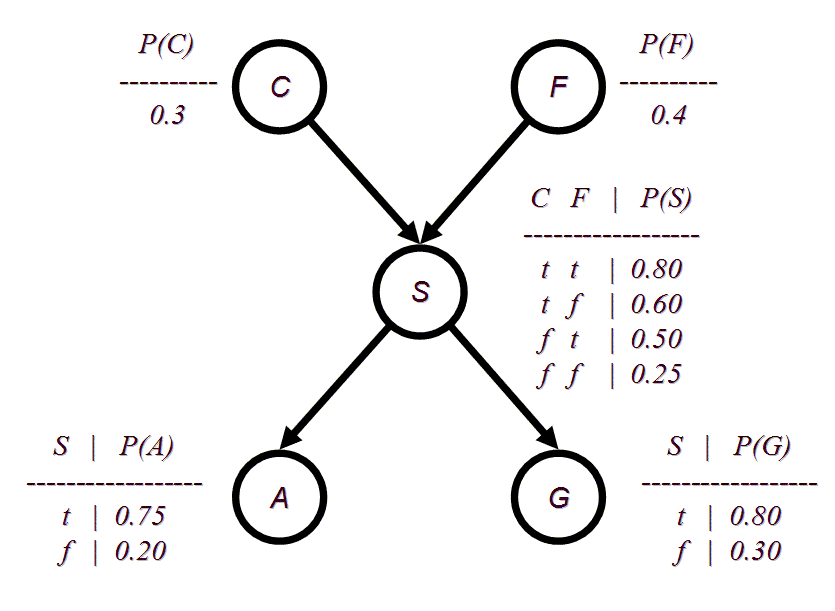
(d) (5 pts.) Using the chain rule, compute the probability P(~g, a, s, c, ~f).
(e) (5 pts) Write, in summation form, the formula for computing P(a, ~f) using inference by enumeration. (You do not need to actually compute the probability.)
(f) (2 pts) What is the conditional independence assumption for a node in a BN?
(g) (3 pts) When are two variables conditionally independent of each other in a BN?
(h) (5 pts) Using the rules for determining when two variables are (conditionally) independent of each other in a BN, answer the following (T/F) for the BN given above (d):
The following table gives a data set for deciding whether to play or cancel a ball game, depending on the weather conditions.
| Outlook | Temp (F) | Humidity (%) | Windy? | Class |
| sunny | 75 | 70 | true | Play |
| sunny | 80 | 90 | true | Don't Play |
| sunny | 85 | 85 | false | Don't Play |
| sunny | 72 | 95 | false | Don't Play |
| sunny | 69 | 70 | false | Play |
| overcast | 72 | 90 | true | Play |
| overcast | 83 | 78 | false | Play |
| overcast | 64 | 65 | true | Play |
| overcast | 81 | 75 | false | Play |
| rain | 71 | 80 | true | Don't Play |
| rain | 65 | 70 | true | Don't Play |
| rain | 75 | 80 | false | Play |
| rain | 68 | 80 | false | Play |
| rain | 70 | 96 | false | Play |
(a) (10 pts.) At the root node for a decision tree in this domain, what are the information gains associated with the Outlook and Humidity attributes? (Use a threshold of 75 for humidity (i.e., assume a binary split: humidity <= 75 / humidity > 75). Be sure to show your computations.
(b) (10 pts.) Again at the root node, what are the gain ratios associated with the Outlook and Humidity attributes (using the same threshold as in (a))? Be sure to show your computations.
(c) (5 pts.) Suppose you build a decision tree that splits on the Outlook attribute at the root node. How many children nodes are there are at the first level of the decision tree? Which branches require a further split in order to create leaf nodes with instances belonging to a single class? For each of these branches, which attribute can you split on to complete the decision tree building process at the next level (i.e., so that at level 2, there are only leaf nodes)? Draw the resulting decision tree, showing the decisions (class predictions) at the leaves.
In this problem, you will gain familiarity with the WEKA (Waikato Environment for Knowledge Analysis) machine learning toolkit. It is widely used in the machine learning community, and provides both a graphical interface and Java API to a wide variety of standard machine learning algorithms. Using WEKA will help reinforce the material we covered in class.
You must download and install WEKA from the following location: http://www.cs.waikato.ac.nz/ml/weka/. The "Getting Started" section of that page has links for information on system requirements, how to download the software, and documentation. WEKA is written in Java and should run on any platform with Java 1.4 or higher.
In addition to the reading that I handed out in class, here is some sites that contain documentation on WEKA:
When you run WEKA, you should choose the use the "WEKA Explorer" when answering these questions. One problem that I sometimes run into is that WEKA needs more memory than java gives it by default. You can use java's "-Xmx" option to have java allocate more memory to the virtual machine. For example "java -Xmx200M ..." would have java allocate a maximum of 200 MB to the virtual machine.
Download the hw6-mushroom.arff data file and load it into WEKA in the preprocess tab. The mushroom task involves identifying poisonous or edible mushrooms from their features. In the classify tab, try out the following classifiers, using 10-fold cross-validation to get accurate estimates of the performance of each algorithm.:
(a) (8 pts) Create a table reporting the classification accuracy of each algorithm on the mushroom data.
(b) (4 pts) On this particular problem, WEKA reported the following performance information for two of the algorithms: (note that your numbers in part (a) may vary)
J48 Decision Tree
|
1-Nearest-Neighbor Classifier
|
Even though the algorithms both have the same reported accuracy, their True/False positive rates are different. For this particular problem, identifying poisonous mushrooms, is one algorithm better? If so, which one? Justify your answer by explaining why one is better or why they're both equally good.
(c) (8 pts) Run the J48 algorithm with and without reduced error pruning on the hw6-zoo.arff data. Explore varying the numFolds variable for reduced error pruning between 2 and 10 folds. You do not need to run every number; just pick a number of samples intelligently.
Plot the performance accuracy as a function of the number of folds in a properly-formatted graph (axes labeled, clear title, etc.). (You cannot generate the plot by hand.) In a few sentences, describe the effect of reduced error pruning on the induced decision tree. Why does reduced error pruning improve the classification accuracy of the decision tree? (Hint: what machine learning phenominon is occurring?) How does the numFolds variable affect the pruning and why?
(d) (10 pts) For this problem, you will create a classifier for some unknown data. The training data is contained in hw6-unknown2-train.arff. You should attempt to construct the best model you can for this training data. You can use cross-validated accuracy to determine your chosen model or any other evaluation criteria you want. You can use any WEKA classifier you want, even those other than the ones we've used in this homework, with any settings. Some classifiers perform dramatically different depending on the settings.
Report the best 10-fold cross-validated accuracy you can on this training data. What algorithm did you use to create the model? Justify any parameter settings you changed. Include a paragraph describing the algorithm you used for creating the model. If you settled on one that we didn't cover in class, you will have to do a bit of outside reading to understand it and be able to describe it. Tell why you think the algorithm you chose did the best.
(Optional Extra Credit)
The real test of machine learning algorithms is taking a learned model and applying it to never-before-seen data to test its effectiveness. The file hw6-unknown2-test-unlabeled.arff contains a number of unlabeled data drawn from the same distribution as the unknown training data you saw in (d) above. Once you've developed your learned model, you can apply it to the new test data. Make sure that the training data set is loaded into WEKA and your classifier options are all set as before. (If you do this immediately after (d), you should only have to do the next instruction.) Change the test option from cross-validation to "Supplied test set" and set it to use the hw6-unknown2-test-unlabeled.arff file for testing. Also, change the "More options..." to "Output predictions" for the data. When you "Start" the evaluation, WEKA will train your model on the training data and output predictions for the unlabeled data.
The classifier output should now have predicted labels for every test instance. Ignore that WEKA tells us that every predition is an error -- it does this because the test data does not have any class labels. The table will look something like the following (the predicted labels are contained in the third column):
=== Predictions on test set ===
inst#, actual, predicted, error, probability distribution
1 ? 1:f + *0.926 0.074
2 ? 2:t + 0.045
*0.955
3 ? 2:t + 0.045
*0.955
... ... ... ... ... ...
Copy this entire table into a text file (ONLY this table, trimming whitespace above and below it) into a text file called <LASTNAME><FIRSTNAME>HW6.out (where <LASTNAME> and <FIRSTNAME> are your names, of course. For example, my file would be called EatonEricHW6.out), and submit it to cs471 hw6.
Just for doing this, you'll get 3 points extra credit on your homework. However, there's an opportunity for more! I'll evaluate the performance of your classifier on the test data by computing the accuracy of your predictions with the true labels for the test data. The five people with the highest test accuracies will get 5 additional extra credit points. The person with the highest score will get 4 more extra credit points.
(In order for this extra credit to count, you MUST have at least made an attempt on all other problems. Doing this extra credit, while it may earn you additional points, is NOT a substitute for skipping problems above.)
Consider the version space defined by the concepts that are a conjunction of the following three attributes:
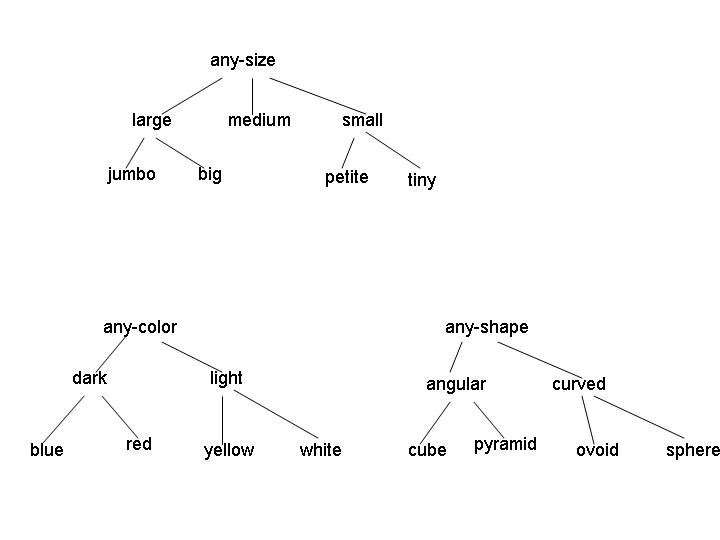
Examples of legal concepts in this domain include [medium light angular], [large red sphere], and [any-size any-color any-shape]. No disjunctive concepts are allowed, other than the implicit disjunctions represented by the internal nodes in the attribute hierarchies. (For example, the concept [large [red v yellow] curved] isn't allowed.)
(a) (5 points) Consider the initial version space for learning in this domain. What is the G set? How many elements are in the S set? Give one representative member of the initial S set.
(b) (5 points) Suppose the first instance I1 is a positive example, with attribute values [jumbo yellow ovoid]. After processing this instance, what are the G and S sets?
(c) (5 points) Now suppose the learning algorithm receives instance I2, a negative example, with attribute values [jumbo red pyramid]. What are the G and S sets after processing this example?