294-7 Reconfigurable Computing -- 2/19/97
(Day 10) Cellular Automata

1 Cellular Automata

A celluar automata (CA) is a computing structure with the following characteristics: The theory of CA was initially developed as a model for describing complex systems whose constituent components are simple, identical cells. Many physical phenomena can be described or approximated in this way. In the context of spatial computing, we use CA's as a style of spatial computing by taking advantage of their collective properties, which make them highly amenable (especially w.r.t. interconnect) to implementations on regular computing structures such as FPGA's.

2 Applications

Candidate applications for cellular automata exhibit high regularity and evolve based on local interactions. The following are some examples of physical systems that are suitable for modeling as CA's (recall original goal of mathematical model): Besides modelling physical systems, CA's are also useful as spatial implementations for certains types of applications: The following sections describe some of these applications in more detail.

3 Toy Example: Life

The canonical, toy example of a cellular automata is the game of life. Life begins with a collection of identical cells that can be in one of two states: live or dead. On each timestep, each cell updates its state based on the state of adjoining cells (neighborhood of 1) using the following rules:

Besides serving as a simple example of a CA, life also demonstrates how a collection of simple cells can exhibit complex aggregate behavior.

4 Example 1: Maze Routing

Maze routing is the problem of finding the least expensive path between a source, S, and a target, T, given obstacles. (Obstacles could also include previously routed wires.) A common way to solve this problem is Lee's Algorithm:

1. Perform a breadth first search (by cost) from S.
2. Record backlinks to previous link.
3. Reconstruct path from backlinks once T is found.

With a path length/cost of n, Lee's algorithm has O(n^2) complexity.

The figure below shows Lee's algorithm in action:

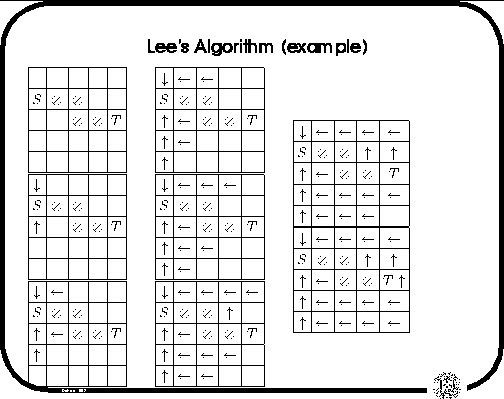Figure 1: Example of Lee's Algorithm

The arrows represent the backlinks to S, as the algorithm performs a breadth first search, starting with elements of distance 1 from S, distance 2 from S, etc. An implementation must also include rules to determine which backlink is marked when multiple cells are adjacent to un unmarked cell.

4.1 Maze Routing CA

To solve the problem of finding a minimal cost path, we first need to be able to encode some notion of cost within the cells of the CA. To do this, we ``encode'' cost in the arrival time, i.e. the time when a cell is first discovered. Because Lee's algorithm uses a breadth first search, this encoding scheme implies that if a cell is rediscovered and is already marked, it should not be modified since the minimal cost for that cell has already been encoded the first time it was encountered.

The basic cell and update rules are shown below:

Figure 2: Basic cell and rules

With an array of cells, a set of rules, and a way to encode cost, two other problems that need to be addressed are: (1) how to shift the image into the CA for computation and (2) how to signal completion once a minimal cost route is found. I/O into cellular automatas is usually significant relative to the cost of computation. Therefore, some care must be taken to minimize these costs. In [RR87], for example, they shift the image into the device in word size increments to reduce I/O costs. Signalling completion seems to be less of a performance issue than I/O. Two possible strategies: (1) on each timestep, check for completion and interrupt the host if done, or (2) interruupt the host after the expected number of path evaluations (timesteps).

4.1.1 Tweaks

Now that we have a simple CA implementation for maze routing, we can augment it by: When the area to be routed fits entirely on the CA, the runtime is linear in n. As with many CA problems, however, quite often the size of CA problem to be solved is greater than the size of the actual computing device. Multi-grid routing and raster processing are two techniques that attempt to preserve the reduced time complexity afforded by CA's in these types of scenarios.

4.2 Multi-grid Routing

With an n x n grid to route and a w x w (n > w) CA array, we partition the grid into windows of size c x c (c = n/w). This allows us to fit a coarse-grain representation of the entire grid on the device and derive a coarse-grain minimal route based on c x c sized blocks. We then perform a second (and perhaps 3rd, 4th, depending on n and w) pass, routing over the coarse-grain blocks that compose the path discovered in the first (previous) step. By limiting of the search space in subsequent passes of the algorithm, we preserve some of the time-complexity gained with a CA implemetnation at the expense of losing some potential routes. A two-phase multi-grid maze route example is given in Figure 3.
Figure 3: Two-phase multi-grid CA

A two-phase multi-grid implementation has a time complexity O(n): O(w) for the first step; O(n) in the second step to route n windows, each with complexity O(w); and an overall complexity of O(w + nw) = O(n). The trade-off here between exploring the entire search space and reducing time-complexity by operating on a coarser granularity is very similar to modelling physical systems with CA's, where precisely operating on single-particles is traded off for operating statistically on particle aggregates.

4.3 Raster Processing of CA

Raster pipelining is based on the observation that given a large CA, we only need to see a small window of the problem to operate. The structure of a raster processing implementation is shown in Figure 4.

Figure 4: Raster processing CA
The data is streamed into the array serially in raster fashion, i.e. row by row. The structure above contains three components: buffers (red) that contain the neighborhood of cells needed to compute the next value of a cell; FIFOs (gray, yellow) for retiming the rows of data so they are available to form neighborhoods as we evaluate cells in raster fashion; and finally a processor (white) that applies rules on a neighboorhood of cells to compute a cell's updated state. Updated cells are streamed out from the processor. Clearly, if an algorithm can be decomposed into multiple distinct operations, we can pipeline structures to reduce execution time. A raster pipeline is shown below:

Figure 5: Raster pipeline CA
With an l stage pipeline and an n x n array, the time complexity of a raster pipeline is O(n^2 + nl). The n^2 term corresponds to the cost of loading the values into the device. A cost of O(nl) is paid for due the nature of the scan lines. One way to reduce the n^2 term might be to minimize the serialization of loading the values. A CA initially might operate on a 3 x 3 array, then a 5 x 5, ..., for instance.

5 Example #2: Design Rule Check

Design rule checking involves the following operations: Here, we focus mainly on tolerance checks. In the examples that follow, assume each unit to be equal to the feature size (lambda). The check described here ensures that all wires are at least 3-lambda wide.

We first partition the mask, M, into 1 x 1 blocks. In the figures that follow, wires are represented as black blocks and unused space is represented as white blocks. For a 3-lambda check, we use a 3 x 3 block (S(3), Q(3)) and perform set operations on it and the mask. The three operations we will need are:

5.1 3-lambda Tolerance Check

1. Open mask with S(3). Anything not in open is an errors (rough check that all wires are at least 3-lambda wide).
2. C = Erosion of mask by S(3).
3. Tag NE corner of each component of C (see figures below for clarification of this step and step 5.)
4. Dilate by Q(3). Any intersections with SW corners of different regions are errors. (see figures below for clarification of this step and step 6.)
5. Tag NW corner of each component of C
6. Dilate by Q(3). Any intersections with SE corners of different regions are errors.

An example of a 3-lambda tolerance check:

Figure 6: A mask containing patterns for the example

Figure 7: An erotion (first step of open) using a 3x3 block, S(3)

Figure 8: A dilation (open complete) using a 3x3 block, S(3)

Figure 9: Differences between the open and the original mask are width errors. This does not catch errors on the narrow diagonal necks, however.

Figure 10: Erode like Figure 7 and tag each NW corner. Note that tagging is done using local cellular information. This results in finding two NE corners on the H-pattern in this example.

Figure 11: Dilate corner from previous step and look at what the dilated corner intersects. This time, we see it does intersect the disconnected diagonal segment and finds the error.

Figure 12: Sanity check showing more examples of diagonal necking and that the algorithm does find the errors (and doesn't signal false errors)

References

[RR87] Thomas Ryan and Edwin Rogers. An ISMA Lee Router Accelerator. IEEE Design and Test of Computers, pages 38--45, October 1987.

2/19/97, BNC <bnc@cs.berkeley.edu>