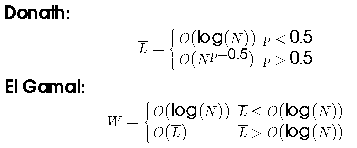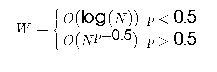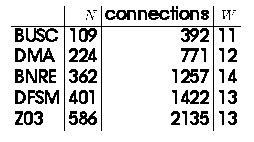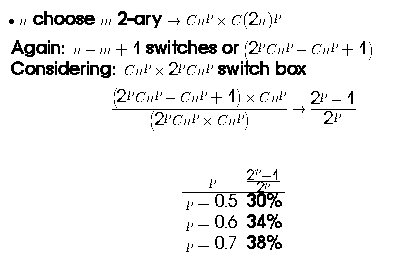Computer Science 294-7 Lecture #13
Interconnect

Notes by Varghese George

1.0 FPGA Model

Fig 1.1 shows the Toronto Symmetric FPGA model used.

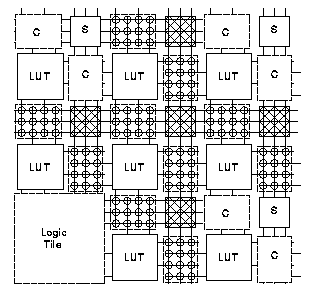
Fig. 1.1 Symmetric FPGA Model
The logic blocks (L block) connect to the horizontal and vertical channels using a connection block (C block). Connections are switched at the intersection of horizontal and vertical channels by a switch block (S block).

1.1 Parameterization

The different parameters of this model are

T - number of sides on which a pin is available
W - tracks per channel
$F$ _s - conections offered per incoming wire. This is also called S block flexibility.
$F$ _c - number of channel wires connected to each logic pin. This is also called C block flexibility.

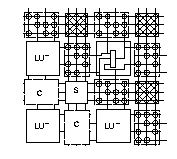
Fig. 1.2 Connections

1.2 Formulation

The steps followed are

Pack the logic blocks into minimal sized array
Global routing is done to obtain the channel width (W) which can provide full routing for this array
$F$ _s and $F$ _c are varied to obtain good routability

1.3 Channel width

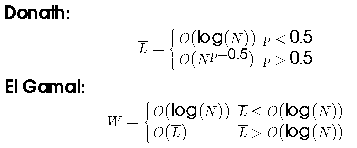
The result from Donath gives the average routing length. This is substituted into the equation from El Gamal to obtain

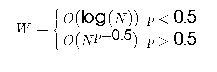
1.4 Connection sides

T = 2 was found to be better as far as the number of tracks is concerned. For T > 2 the improvement was negligible.
Some points to be noted in this aspect are

Increasing T increases the cell area, how does it compare to the increased wiring area for smaller T ?
For this experiment the functional equivalence of the LUT inputs were not exploited by the router.

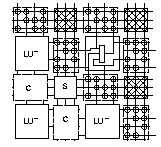
Fig 1.3 L block connections for T=2

1.5 What switches do we need ?

Assume $F$ _c = W , each input needs to connect to one of wires on each of the three adjacent channels.

Types of switches

1.5.1 Universal switch box

The universal switch box can connect any set of inputs to their target output channels simulataneusly. It provides adequate switching to make any routes which do not exceed the channel capacity, assuming $F$ _c = W.

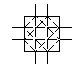
Fig. 1.4 Universal switch box
This can be built with $F$ _s = 3 (6W switches)

1.5.2 Xilinx switch box

It is 6W switches, but is not universal.

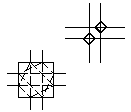
Fig. 1.5 Xilinx switch box

1.5.3 Brown and Rose

Brown and Rose use an antisymmetric switch box, which is close, but not exactly a Universal switch box.

1.5.4 Comparison

Asymptotically, the Universal switch box routes 25% more connections as compared the Xilinx switch box. Fig. 1.5.3 illustrates a routing example which is not possible with the Xilinx switch box.

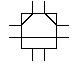
Fig. 1.6 Routing possible with Universal, but not Xilinx

1.6 Depopulating input connections

By exploiting the functional equivalence of the LUT inputs, it can be shown that for a k-LUT, and channel width of W, only W-k+1 connections are needed per input.

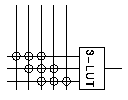
Fig. 1.7
Eg. W = 10, k = 4, gives $F$ _c = 7 ( $F$ _c = 8 on average when include fully populated output).
This gives us the guaranteed routing values of
$F$ _s = 3
$F$ _c = W - k + 1 (inputs)
$F$ _c = W (outputs)

2.0 Experimental Results

The details of the benchmark circuits used are given,

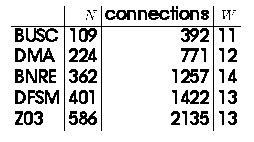
Fig. 2.1 and Fig. 2.2 gives the results.

Fig. 2.1 Percent completion versus $F$ _s for the circuit BNRE

Fig. 2.2 Average $F$ _c/W for 100% completion versus $F$ _s

2.1 Reccomendations

Based on the results the following conclusions are derived

3 <= $F$ _s <= 4
0.7 <= $F$ _c/W <= 0.9

Note the following

not using Universal switch box
231 switches/LUT for the minimum configuration
the experimental values are not any tighter than the values identified by looking at switches required for guaranteed routing

3.0 Segmented Routing

The previous model is revised to include segments

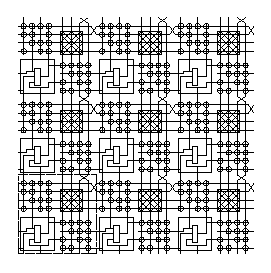
Fig. 3.1 Segmented Routing

3.1 Results

Fig. 3.2 Average path length versus segmentation
According to this result there does not seem to be any benefit to using wires longer than 4. A point to note is that the above result is in terms of the average interconnect length, not the critical path length.

4.0 The Xilinx routing

If you look at the Xilinx 4K routing, you will notice

$F$ _c(input) > F_c(output)

$F$ _c(input) = W

Fig. 4.1 Xilinx 4K routing
Fig. 4.2 gives the number of switches/LUT ofr the XC4000 series

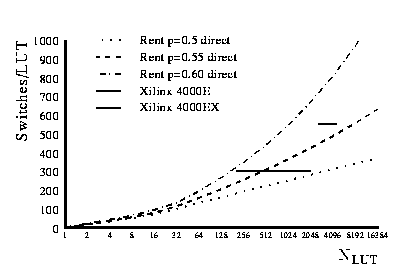
Fig. 4.2 Xilinx 4K switches
For the XC4000E it is approximately 300, and for the XC4000EX, 550.

5.0 Hierarchical FPGA

A model similar to that used in the previous class is used here.

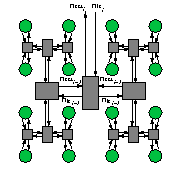
Fig. 5.1 Hierarchical FPGA

Fig. 5.2
Calculating the flexibility required to guarantee routing

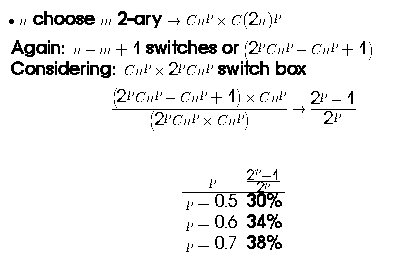
5.1 Experimental Result

Aggarwal and Lewis did a study to determine the switch depopulation possible with hierarchical FPGAs (HFPGA), while mantaining 100% routability. The results from their empirical experiments suggests

$F$ _c = 3 at the lower levels, and 3-5 in the upper levels of hierarchy
60% switches in symmetric (length 1 lines only)

Note

the channel widths are not given
gives log switching delay (worst-case)

6.0 Summary

We looked at

symmetric, mesh routing topology
hierarchical routing topology
routing model
requirements to route
opportunities to depopulate switches
compare commercial FPGA routing topology

References

Aditya A. Agarwal and David Lewis. Routing Architectures for Hierarchical Field Programmable Gate Arrays. In Proceedings 1994 IEEE International Conference on Computer Design, pages 475--478. IEEE, October 1994.
Jonathan Rose and Stephen Brown. Flexibility of Interconnection Structures for Field-Programmable Gate Arrays. IEEE Journal of Solid-State Circuits, 26(3):277--282, March 1991.
XC4000 Series Field Programmable Gate Arrays, pages 4-{5-6} and 4-{31-40}.
FLEX10K Embedded Programmable Logic Family Data Sheet, ver. 2, pages 31, 40, 51-54, 63-65, 69-70, 72, and 75.
Vi Cuong Chan and David M. Lewis. Area-Speed Tradeoffs for Hierarchical Field-Programmable Gate Arrays. In Proceedings of the 1996 International Symposium on Field-Programmable Gate Arrays, pages 51--57. ACM/SIGDA, February, 1996.
Yao-Wen Chang and D. F. Wong and C. K. Wong. Universal Switch-Module Design for Symmetric-Array-Based FPGAs. In Proceedings of the 1996 International Symposium on Field-Programmable Gate Arrays, pages 80--86. ACM/SIGDA, February, 1996.
Muhammad Khellah, Stephen Brown, and Zvonko Vranesic, "Minimizing Interconnection Delays in Array-based FPGAs," In Proceedings of the 1994 Custom Integrated Circuits Conference, pages 181-184, San Diego CA, May 1994. [PS]
Stephen D. Brown, Robert J. Francis, Jonathan Rose, and Zvonko G. Vranesic. Field-Programmable Gate Arrays. Kluwer Academic Publishers, 101 Philip Drive, Assinippi Park, Norwell, Massachusetts, 02061 USA, 1992.
André DeHon. Entropy, Counting, and Programmable Interconnect. (Shorter version in FPGA'96). [HTML] [TR PS] n.b. The switching requirements for the m choose k switching block (which seemed to confuse people in lecture) is detailed in the appendix in this TR.

Back to main page

Computer Science 294-7 Lecture #13 Interconnect