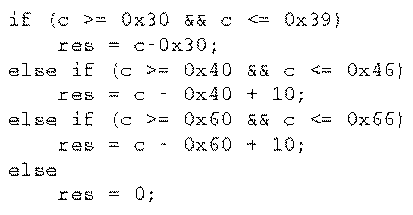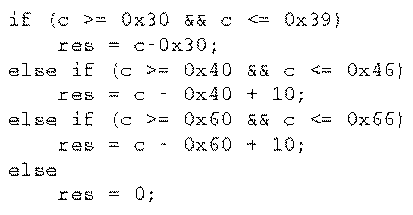Computer Science 294-7 Lecture #26
Everything Else...: Control


Notes by Luca Carloni


1. Control

1.1 Definitions

With Control we intend the point where the data affects the instruction stream (instruction selection). Notice that we can have instruction stream sequence without control when we know statically which decision to take at a certain point. Control examples include: A Primitive Instruction(pinst) is a collection of bits which tells a bit-processing element how to perform; possible directions can be: A Configuration Context is a collection of all the bits (all the pinsts) which describe the behavior of a general-purpose machine on one operation cycle.

1.2 Why Control?

The leading discussion question is

``why do we have (want) control in our architecture?''

The answer is `` to minimize the amount of instantaneous computation we have to do at a given time instant''

Moreover, consider that static interconnect and static (data independent) instruction sequencing can be seen inherently as ``control''.

1.3 Design Generalization

We must ``generalize'' our design to handle all potential inputs or computing scenarios. On the other hand, what we need to do for any given input usually is much smaller than the general case. Hence, we have 2 ``control options'':

1.4 An Example: ASCII HEX -> Binary Conversion

Consider the task of converting an ASCII Hex digit into binary. The following figure describes the basic computation required which is characterized by a large amount of data dependent branching.

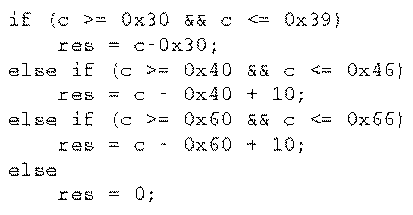
Fig. 1.1 ASCII HEX -> Binary Conversion

The following picture illustrates a possible implementation having 11 4-LUTs and a depth equal to 4.

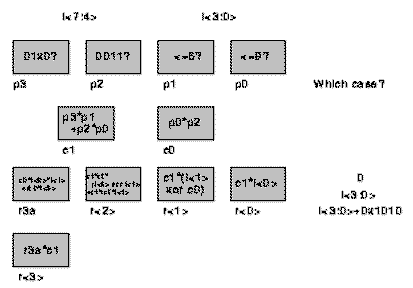
Fig. 1.2 Local Control Implementation

Notice that counting the LUTs doesn't really tell us the cycle-by-cycle computing needs, since in general the number of LUTs is greater then the LUT evaluations produced.

Note also that local control can only exploit resources which data has control over in the architecture. For example, if we attempt to unify a+b+c+d and e+f+g+h, 3 4-LUTs are required (2 for computing and one for selecting the result. Notice that a naive mux implementation could lead to multiplex the inputs and share the OR, resulting in a 5 4-LUTs design. In general, it is not convenient to multiplex input data and share an operator if the operator is ``small''.

1.5 Task Description Hierarchy and Instruction Selection Control

The ``local control'' signals can be packaged together into a ``pinst'' for an interpreter which resides one level up in our design hierarchy.

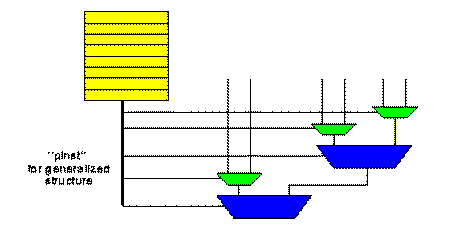
Fig. 1.3 Building Interpreters within the Task Description Hierarchy

This can lead to some confusion between ``instruction'' control and ``local control''. For now, we're making the distinction that logic controlled by other logic built at the same level is ``local control'', whereas logic controlled by instruction memory is ``instruction control''.

Fig 1.4 illustrates the adoption of Instruction Selection Control for the case of the previous example. An implementation with no instruction control requires 4 4-LUTs and has depth equal to 4 with 4 contexts . Using instruction control we need 6 4-LUTs but we can reduce to 3 the depth with 4 contexts.


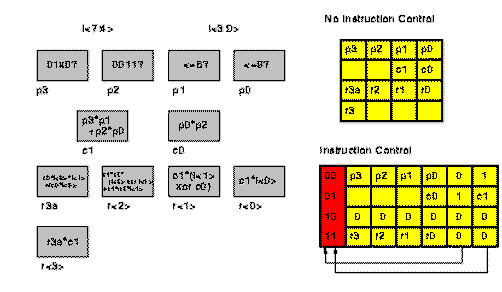
Fig. 1.4 Instruction Selection Controls

Fig. 1.5 categorizes illustrates the Architecture Instruction Taxonomy reporting different architectures together with their granularity (w,n_v), the local instruction storage depth (c), the number of distinct instructions per control thread (n) and the number of control threads (m) supported. This taxonomy elaborates the multiple data portion of Flynn's classic architecture taxonomy by segregating instructions from control threads and adding granularity.


Fig. 1.5 Architecture Instruction Taxonomy

1.6 Control Formulation

The following points are key to understand the control problem: A question remains open: How do we formulate the control in a clean way? The next section introduces the FSM model which is the most used for this goal.

2. Finite State Machines (FSMs)

2.1 FSMs specify controllers

A controller is usually specified by means of a Finite State Machine(FSM) that is a discrete dynamical system translating sequences of input vectors into sequences of output vectors. FSMs are a formalism growing from the theory of finite automata in Computer Science. An FSM has a set of states and of transitions between states; the transitions are triggered by input vectors and produce output vectors. The states can be seen as recording the past input sequence, so that when the next input is seen a transition can be taken based on the information of past history.

An FSM can be implemented with deep multi-context (microcode) or can be implemented as multilevel (unifying state logic). The FSM model allows us to explore some of the ``local control'' unification versus ``instruction control'' tradeoffs.

2.2 FSMs and multi-context: an Example

The following figure illustrates a simple 4-state FSM. The conventional single-context implementation requires four 4-LUTs, one to implement each of Dout and NS1 and 2 to calculate NS0.

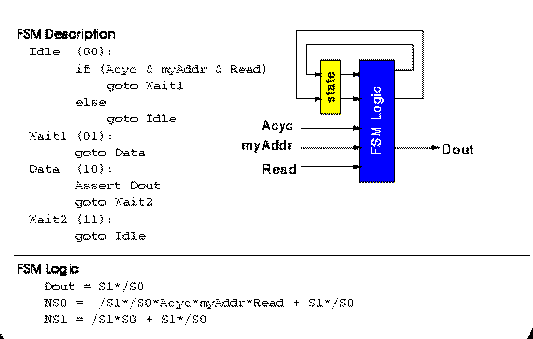
Fig. 2.1 A FSM Example

Figure 2.2 shows a two-context implementation of this FSM. The design is partitioned into 2 separate circuits based on the original state variable S1 . The two circuits are placed in separate contexts and NS1 is used to select the circuit to execute as appropriate. Each circuit only requires three 4-LUTs, making the overall design smaller than the flat, single context implementation.

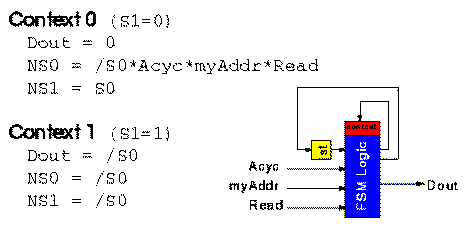
Fig. 2.2 A two-context implementation of the given FSM

2.3 Full Partitioning

In the most extreme case, each FSM state can be assigned its own context (Full Partitioning) and the next state computation simply selects the appropriate next context in which to operate. Figures 2.3 and 2.4 report the Full Partitioning experiments showing respectively the reductions in area and path delay which result from state-per-context multiple context implementation of the MCNC FSM benchmarks. FSMs were mapped using Mustang, while logic minimization and LUT mapping were performed with Espresso, Sis and Chortle. For single-context FSM implementation, both one-hot and dense encodings were synthesized and the best mapping was selected. The multi-context FSM implementations use dense encodings so the state specifications can directly serve as the context select. For multi-context implementations, delay and capacity are dictated by the logic required for the largest and slowest state.

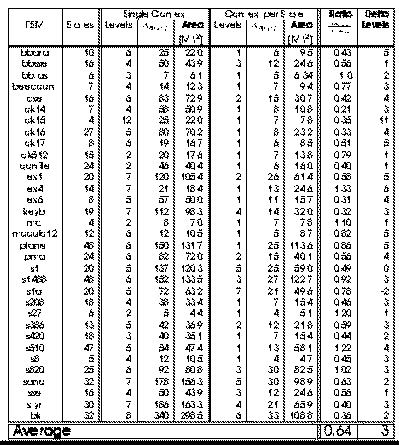
Fig. 2.3 Full Partitioning of MCNC FSM Benchmarks (Area Target)

On average, the fully partitioned, multi-context implementation is 35-45% smaller than the single context implementation. The multi-context FSM implementation generally have one or two fewer logic levels in their critical path than the single-context implementation when mapped for minimum latency. The multi-context implementations have an even greater reduction in path length when mapped for minimum area. The multi-context FSMs, however, require additional time to distribute the context select and perform the multi-context read. Globally the multi-context and the single-context implementations run at a comparable speed when the multi-context implementation has one fewer LUT delays in its critical path than the single-context implementation.


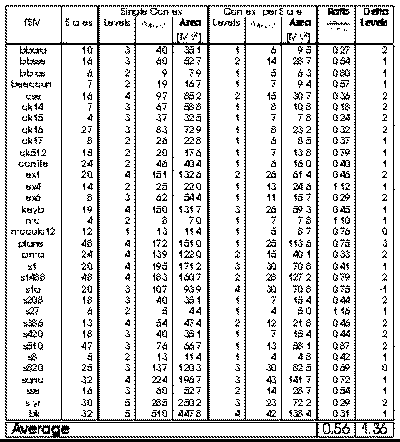
Fig. 2.4 Full Partitioning of MCNC FSM Benchmarks (Delay Target)

2.3 Partial Temporal Partitioning

Full partitioning may not be optimal area point. The capacity utilization and delay are often dictated by a few of the more complex states. It is often possible to reduce the number of contexts required without increasing the capacity required or increasing the delay. Fig. 2.5 and 2.6 show the LUT count, area and delay versus the number of contexts employed for the cse FSM benchmark. The FSM was partitioned into various number of contexts and optimized for area or path delay, respectively. These partitions were obtained by partitioning along mustang assigned state bits starting with a four bit state. We notice that the full state-per-context case is not always the most area efficient mapping. In the cse example, the reduction in LUTs from 8 to 11 or 11 to 16 contexts saved less area than the cost of the additional context memories. In conclusion we can say that moderate context FSM performs better than either extreme (single context, -context).

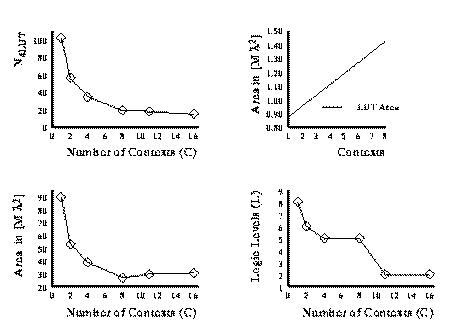
Fig. 2.5 Area and Delay versus Number of Contexts for cse FSM benchmark (Area Target)


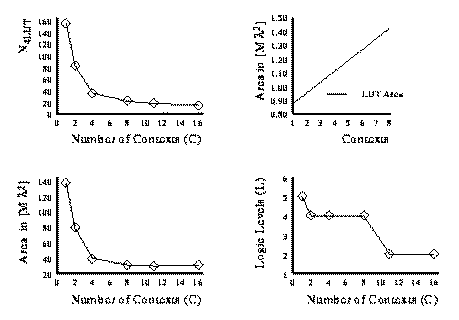
Fig. 2.6 Area and Delay versus Number of Contexts for cse FSM benchmark (Delay Target)

2.4 Using ROMs to implement FSMs

We can implement a FSM with a ROM as show in the following figure.

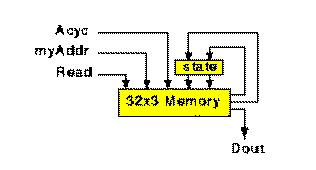
Fig. 2.7 Using ROM to implement a FSM

Fig. 2.8 show the different area requirement for the MCNC benchmarks by comparing FPGA and an 8-context DPGA with ``optimal'' memory implementation (a memory with size matching FSM requirements

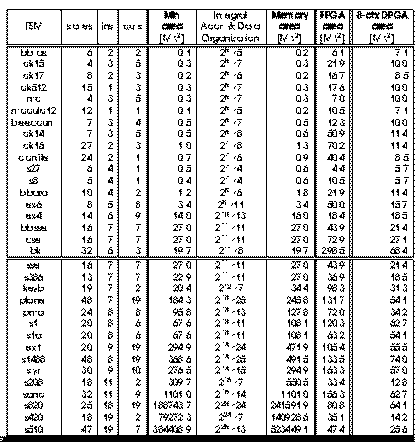
Fig. 2.8 Memory v/s FPGA v/s DPGA FSMs

For small FSMs (above the double line), the memory implementations are most compact. For larger FSMs (below the double line -- total number of inputs greater than 11), the 8-context DPGA are smaller than both the memory and FPGA implementations in all cases. This shows that the hybrid scheme which uses some instruction control and some local control is generally more area efficient than either extreme. (See reading [DeHon96] for more details on this sequence of examples.)

Back to main page